Difference Image Photometry
This a quick and simple introduction to the technique that we developed
and published in
Tomaney and Crotts 1996, which
describes in much more detail the scientific motivation, implementation
and results. Although this was developed for astronomical imaging,
in principle it could be applied in other areas including some medical
and terrestrial imaging applications.
Astronomical photometry on digital images
has conventionally been done by summing the
flux around individually identified stars. The sum is typically
evaluated by fitting the image Point Spread Function (PSF a.k.a. the
2D impulse response)
to the star's intensity distribution. In
crowded stellar fields the stars can be too blended to identify
individually and must be discovered through an iterative process
of subtracting off the brighter stars (using the PSF estimate) to reveal
fainter stars which are then subtracted in the next iteration (refining the PSF
estimate with each iteration).
The most widely used
codes since the 1980s using this algorithm are DAOPHOT by Peter Stetson and
DoPHOT
and their derivatives.
However, in extremely dense stellar fields these algorithms fail
because even the brightest stars are hopelessly blended. This is the
situation when imaging galaxies from the
ground, for example.
However, if we are only interested in detecting variability in the
small fraction of stars or sources in the sky that exhibit such behaviour
then a sensible approach is to remove the non-varying component of the
images by subtracting a high signal-to-noise
reference image, thereby isolating the variable objects in the resulting
difference image.
Prior to subtraction however the images must be matched in a three
step process involving:
- precise (subpixel) alignment,
- PSF matching,
- and intensity matching
of one image to the other.
In typical astronomical images the most difficult step is
the PSF matching stage which depends sensitively on the focus
(which can vary across the camera,
click here),
tracking of the telescope as well as the atmospheric conditions during
the exposure which blurs the stellar images and yields very different
PSFs for each image (for an illustration from
MACHO images
click here).
(In other applications the challenge might be
alignment due to geometric distortion, in say medical imaging, or
intensity normalisation in terrestrial imaging.)
The key to the success of the technique is correcting
all these factors precisely so that genuine variability
can be distinguished from artifacts in the subtraction which would
otherwise completely dominate the difference image.
Here's some examples of the technique at work:

The top left image
is a deep exposure of 0.2 by 0.2 sq. degrees of the nearby galaxy M31
which extends about 1 by 4 sq. degrees on the sky. The bright nucleus
of the galaxy is off to the right of the image. This image contains
about 10 million stars detected at high significance. The top right
image is a blow-up of the indicated subimage on the left with the
underlying galaxy background light subtracted out to highlight the
small scale structure. Aside from a small number of bright foreground
objects and stars the underlying mottled structure belongs to the stars in the
galaxy. The variation in light to dark are the so-called surface
brightness fluctuations (SBFs) and reflect not individual stars
but the random variation in the number of stars in each pixel
of the image.
The bottom left image shows the residual difference image
after a reference image made from the previous night has been
subtracted using this technique; essentially all
of the underlying structure seen in the previous image is removed.
The bottom right
image repeats the process for an image taken a month later
using the same reference image. Unlike the previous image this
image contains many isolated point sources,
indicated by the bright and dark spots, which are stars that have
respectively brightened or faded over the course of the month.
At this stage it becomes relatively straightforward not only to detect
all the variable stars but to measure accurately their
changes in intensity in a sequence of difference images.
The following figure is one of my most overused overheads, basically
because it is a spectacular demonstration of how sensitive the technique
can be. The upper panel images on the left are subimages
from similar
exposures of M31 as seen in the previous figure and taken 50 minutes
apart. The lower panels are their respective difference images after
a higher signal-to-noise reference image from another night (not shown)
with better spatial resolution has been subtracted after the image
matching steps. The residuals in these images are essentially random
shot noise (close to the photon noise limit), with the exception of the
bright star in the corner, but the second image reveals a clear detection
of a rapidly brightening star. What is most striking is
how in the upper frames the appearance of the object is completely
invisible to the eye. This is because its intensity in the second
image is only a fraction of the random SBF variation in intensity
in the image pixels.

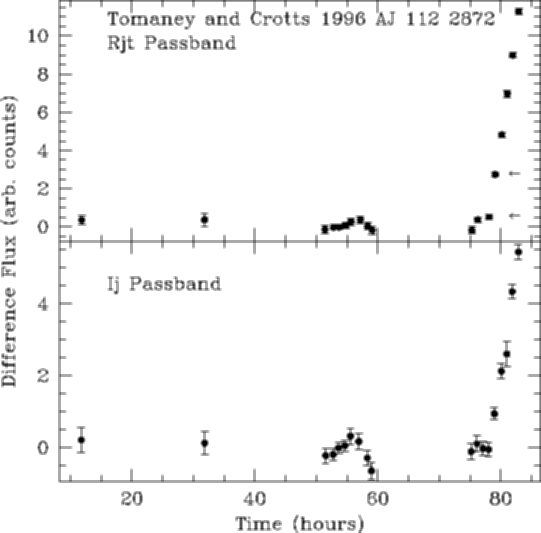
The plots on the right show how this object varied with time as
measured from a series of difference images taken in two passbands.
Note how even at a low level the behaviour of the object is
reproduced in both bands.
The points corresponding to the two images on the left are indicated
with two arrows in the upper panel. (The flux difference between these
two points corresponds to an R magnitude of 21.1 in seeing of FWHM 1.1"
which is less than 1.5%
of the underlying galaxy background flux at this position. One sigma
variations in flux are 0.1% modulations of the background light
and equivalent to a magnitude of 24.4.)
In this case this object was
possibly an erupting nova, but our coverage was insufficient to
classify it. However, even at its peak brightness in our measurements
the object could not be detected with conventional approaches with
confidence or measured with any precision.
Thus this kind of method allows astronomical variability surveys to
be extended into regimes which are not limited to resolved stars,
greatly expanding their potential. This is particularly true of
microlensing surveys which typically need to monitor millions of stars
on a nightly basis to detect microlensing events. In addition, it
is not limited to simply intensity variability of objects but is
also applicable to detecting moving objects.
DIFIMPHOT software page.
Back to my
home page.



